I recently wanted to apply online for postal vote for the European elections. To complete the application I needed to know my 13 digits social security number. But when I went to type it in, I realised mine only had 11 digits. What?? Well, apparently it was changed in 2014 and I hadn’t realised until now… Well done me.

Not being particularly keen to call my commune and ask for it, it came to mind that there is probably an algorithm to calculate those last two digits. And as a matter of fact, there is! As can be seen on the CCSS website, the social security number is composed of 6 parts:

AAAA: year of birth
MM: month of birth
DD: day of birth
XXX: a 3 digits random number
C₁: a check digit obtained with the LUHN 10 algorithm
C₂: a check digit obtained with the VERHOEFF algorithm.

The Luhn algorithm is a simple checksum algorithm used to validate a variety of identification numbers. It is designed to check against typos and accidental errors. The Verhoeff algorithm is also a checksum formula.

Luhn algorithm

Let suppose that I am a person who was born the 12th of June 1976 and that my 11 digit social security number was 1976 06 12 123. How to obtain C₁?

Starting from the last digit on the right, double every other digit. If the result of adding is greater than 9, subtract 9 from it.
1976 06 12 123 => 2956 06 22 226
Add all of the digits.
2956 06 22 226 => 42
Take the unit digit and subtract it from 10.
42 => 10 - 2 = 8

In this case, the C₁ digit is equal to 8.

Here is a Python function that can be used to calculate C₁ from the string containing the 11 digit social security number (in this case "19760612123"):

import numpy as np

def luhn10(x):
        """ 
        Calculates the checksum digit for a sequence of digits using the Luhn10 algorithm.
        :param x: a string of digits
        :return checksum: int
        """

        x_arr = np.asarray(list(x), dtype=np.int16)
    
        # Douple every other digit starting from the right and taking the modulo 9 where needed
        x_arr[::-2] = 2*x_arr[::-2]%9 
    
        # Summing all the digits
        total_sum = np.sum(x_arr)
    
        # Subtracting the unit digit from 10 
        checksum = 10 - int(str(total_sum)[-1])
    
        return checksum

Verhoeff algorithm

Now let’s obtain C₂. In order to use this algorithm, 3 tables of numbers are needed. These correspond to the multiplication, inverse and permutation tables of the symmetry operations in the D₅ group (i.e. rotations and reflections of a regular pentagon). It is not too important to understand how these tables are generated for the purpose of this algorithm, as they are usually implemented as a look up table and not computed on the fly. The tables are shown in the figure below:

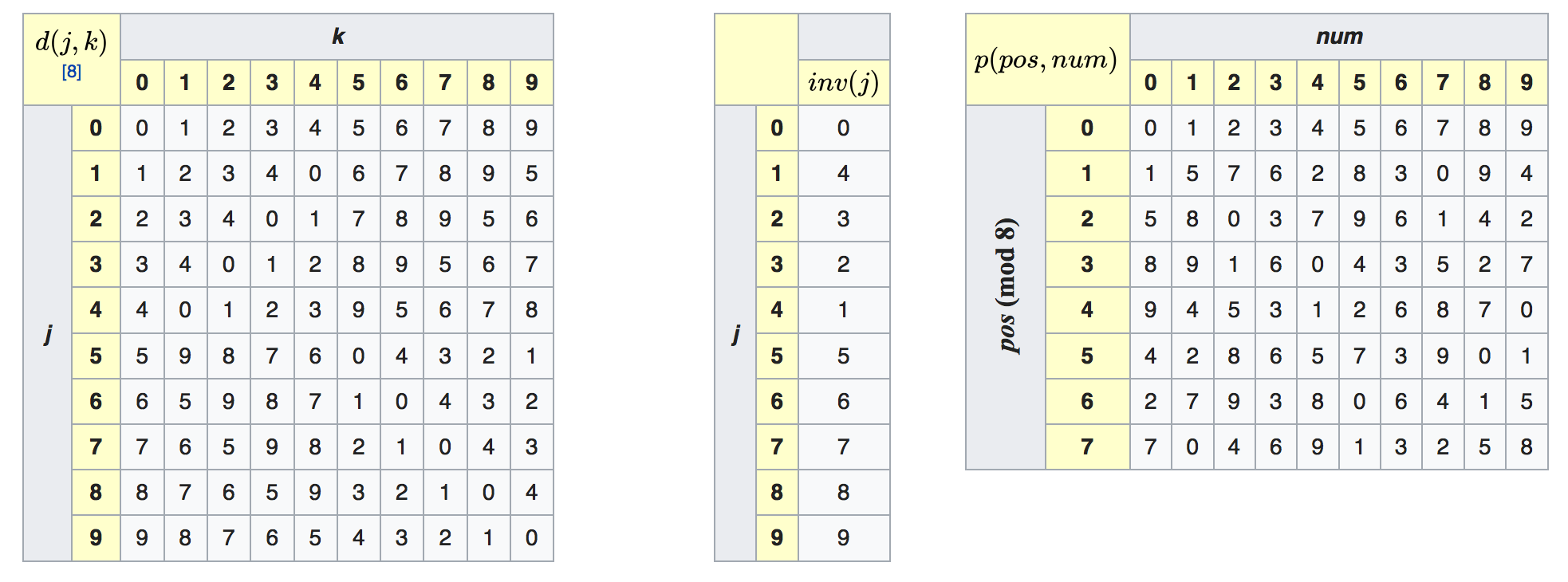
So, C₂ is calculated as follows.

Inverse the order of the digits:
1976 06 12 123 => 321 21 60 6791
For the index $i$ of each digit $N_i$ in the social security number (in this case, for example, $N_0 = 1$ and $N_4 = 0$) compute: $$d(c, p(i \mod 8, N_i))$$
where $c$ is initialised to zero, $d$ is the multiplication table (table of the left in the image above) and $p$ is the permutation table (table on the right in the image above).
The checksum number is then obtained by doing $inv(c)$ where $inv$ is the inversion table (table in the middle in the image above).

So, in this case the C₂ digit is equal to 6. Here is a Python function that can be used to calculate C₂ from the string containing the 11 digit social security number (in this case "19760612123"):

import numpy as np

# Tables obtained from https://en.wikipedia.org/wiki/Verhoeff_algorithm
verhoeff_table_d = ( 
    (0,1,2,3,4,5,6,7,8,9),
    (1,2,3,4,0,6,7,8,9,5),
    (2,3,4,0,1,7,8,9,5,6),
    (3,4,0,1,2,8,9,5,6,7),
    (4,0,1,2,3,9,5,6,7,8),
    (5,9,8,7,6,0,4,3,2,1),
    (6,5,9,8,7,1,0,4,3,2),
    (7,6,5,9,8,2,1,0,4,3),
    (8,7,6,5,9,3,2,1,0,4),
    (9,8,7,6,5,4,3,2,1,0))
verhoeff_table_p = ( 
    (0,1,2,3,4,5,6,7,8,9),
    (1,5,7,6,2,8,3,0,9,4),
    (5,8,0,3,7,9,6,1,4,2),
    (8,9,1,6,0,4,3,5,2,7),
    (9,4,5,3,1,2,6,8,7,0),
    (4,2,8,6,5,7,3,9,0,1),
    (2,7,9,3,8,0,6,4,1,5),
    (7,0,4,6,9,1,3,2,5,8))
verhoeff_table_inv = (0,4,3,2,1,5,6,7,8,9)

def verhoeff(x):
    """ 
    Calculates the checksum digit using the Verhoeff algorithm.
    :param x: string of digits
    :return checksum: int
    """

    x_arr = np.asarray(list(x), dtype=np.int16)

    # Initialising the checksum number to 0
    checksum = 0 

    # Operations using the tables
    for i, digit in enumerate(x_arr[::-1]):
        permutation = verhoeff_table_p[(i+1)%8][digit] 
        checksum = verhoeff_table_d[checksum][permutation]

    return verhoeff_table_inv[checksum]

So, the old social security number 1976 06 12 123 would become 1976 06 12 123 86.